Trie Structures

トライは抽象的なデータ構造であり，実際に構築する場合， 具体的なデータ構造を考える必要があります． 以降の説明では，具体的なデータ構造のことを， 単純にデータ構造と記述するものとします．

トライの単純なデータ構造として，配列構造とリスト構造があります． 文字通り，配列構造はトライを配列により実現し， リスト構造はトライを連結リストにより実現します． また，配列構造の利点は高速なことで，リスト構造の利点はコンパクトなことです．

配列構造とリスト構造の説明では，以下に示すトライを例として使います．

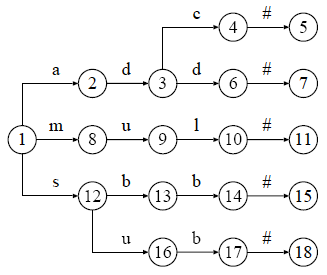
図 1 ： "adc", "add", "mul", "sbb", "sub" を登録したトライ

図 1 のトライを配列構造により表現すると， 以下のようになります．図中の数字は節番号と対応していて， 1 列目の a の段が 2 になっているのは， 節 1 から文字 'a' と対応する枝を辿ることで，節 2 に到達できることを表しています．空白になっている部分は， 対応する枝が存在しないことを表しています．

図 2 ： 配列構造によるトライの例

配列構造の特徴は，一度のアクセスで枝の確認ができることです． この特徴により，探索にかかる時間計算量は， 文字列の長さ，もしくは木の深さで抑えられることになります． つまり，理論的には，キーの数が増加しても，検索時間を維持できます． 実際のところは，キャッシュの効率などによる影響があるため， キーの数が増加するに従って，検索時間は徐々に長くなります．

配列構造は，図 2 を見れば一目瞭然ですが， 空の部分がほとんどで，メモリ消費が大きくなるという欠点があります． そのため，実際に利用する機会は，ほとんどないと思います．

最近の CPU では，キャッシュのサイズが 1MB を超えていることが多く， データがキャッシュに収まるかどうかにより， 実際の処理にかかる時間が大きく変化します． トライも例外ではなく，実際に利用する部分がキャッシュに収まるように， コンパクトに実現することが高速化につながります． このことを考慮すると，高速な実装が必要な状況においても， 配列構造はあまりおすすめできません．

図 1 のトライをリスト構造により表現すると， 以下のようになります．図中の下方向への矢印（ポインタ）は子を指していて， 横方向の矢印は兄弟を指しています．例えば，節 1から 文字 's' と対応する枝を辿って 節 12 に移動したい場合， 節 2, 8 を経由することになります．

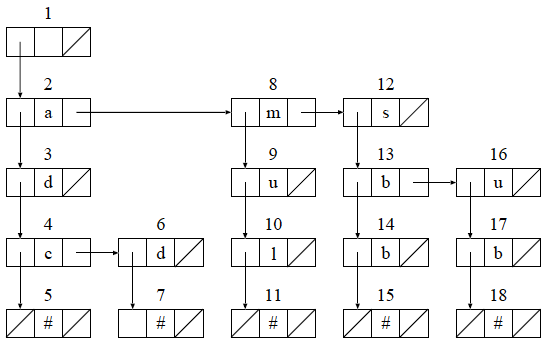
図 3 ： リスト構造によるトライの例

リスト構造の利点は，配列構造と比べて，かなり少ないメモリで トライを実現できることです．ただし，枝の確認にかかる時間計算量が， 枝の数に比例して増加します．そのため，キーの数が増加すると， 検索時間が長くなるという欠点があります．

他にもトライを実現するための実現するためのデータ構造があります． ダブル配列については別に説明する予定ですので， ここでは二分探索木を使ったものを紹介します．

兄弟の関係にある節を二分探索木に格納したトライを 図 4 に示します． Ternary Search Tree という名称があるようですが， リスト構造によるトライを改良したように見えるので， このような説明にしてみました．

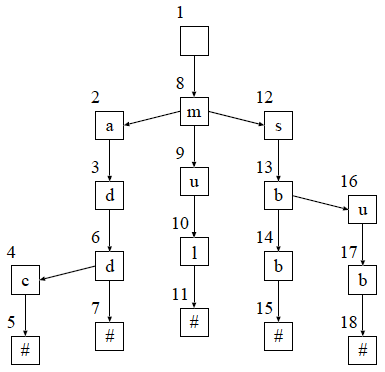
図 4 ： 二分探索木によるトライの例

枝の確認にかかる時間計算量が対数オーダになるので， リスト構造より高速になります．ただし，それぞれの節が持つポインタの数が 増加するので，メモリ消費は多くなります．