Trie

トライ（ Trie ）とは， 自然言語処理やコンパイラ，フィルタリングなどに用いられている木構造です．

二分探索木などとは異なり，文字単位で探索が進行するので， 入力文字列の前方部分と一致するキーを列挙したり， どの文字まで探索に成功していたかという情報を取得したりできます． また，キー数の増加によって検索速度が遅くなりにくいという特徴もあります．

トライは文字列を格納するのに適した木構造です． トライの節（ Node ）あるいは 枝（ Arc ）には 文字が付与されていて（ Label ）， 根（ Root ）から 葉（ Leaf ）への 経路（ Path ）上の文字を連結することにより， 登録されている文字列を復元することができます． 例えば，三つの文字列 "bird", "bison", "cat" を登録したトライは以下のようになります．

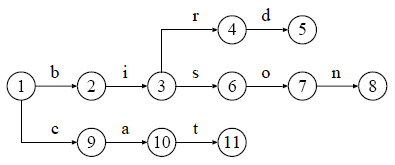
図 1 ： "bird", "bison", "cat" を登録したトライ

図中の節についている番号は，すべての節を一意に識別するためのもので， 節番号などと呼びます． 根である節 1 から 葉である節 8 までの経路上の文字を連結すると， 文字列 "bison" が復元されます． 同様に，節 1 から 節 5 までの経路が 文字列 "bird" と対応していて， 節 1 から 節 11 までの経路が 文字列 "cat" と対応しています，

トライから文字列を検索したい場合は， 先頭の文字から順に対応する節（あるいは枝）を辿っていき， 葉に到達できるかどうかを確認します． 途中で対応する節がなければ文字列が登録されていないことが分かり， 葉に到達できれば登録されていることが分かります． すなわち，対応する経路が存在するかどうかを確認することにより， 文字列を検索することができます．

トライ上の経路のことを遷移と呼び， 経路が存在することを「遷移が定義されている」と表現することがあります． また，枝を辿って節を移動することを「遷移する」や「遷移を辿る」などといい， 「節 s から文字 c により節 t に遷移する」 のように使うことがあります． ダブル配列に関する論文では，節 s から 文字 c による節 t への 遷移が定義されていることを g( s, c ) = t で表し， 定義されていないことを g( s, c ) = fail で表すことが多いようです．

図 1 のトライに 文字列 "bison" が登録されているかどうかを 確認する場合について説明します． 探索は，根である節 1 から始まります． まず，文字列 "bison" の一文字目である 文字 'b' と対応する枝があるかどうかを確認します． この例では，節 2 への枝が 文字 'b' と対応しているので， 節 2 へと移動します． 同じように，文字列 "bison" の構成文字を先頭から順に取り出し， 対応する枝が確認できれば節を移動していきます． 節 2 から文字 'i' と対応する枝を辿って節 2 に移動し， 以降，節 6, 7, 8 と移動することになります． 節 8 が葉になっていることから， 文字列 "bison" が登録されていることが分かります．

トライによる検索速度がキー数の増加によって遅くなりにくい理由は， 検索文字列と対応していない経路を参照する必要がないからです． 例えば，図 1 のトライから 文字列 "bison" を検索する場合， 節 4, 5, 9, 10, 11 の存在を無視することができます． このことから，トライの検索時間は，「枝の確認にかかる時間計算量を O(1) にできれば」という条件がつきますが， 文字列の長さのみに依存することになります．

トライの概要について説明しましたが， これまでの説明に従ってトライを構築してみると， 致命的な問題があることが分かります． それは，ある文字列が登録されているとき， その前方部分からなる文字列を登録できないという問題です． 例えば，文字列 "birdie" を登録してしまうと， 文字列 "bird" を登録できなくなります． これは，文字列 "bird" と対応する経路を辿っても， 葉に到達することができないからです．

この問題を解決する手段としては，キーの終端を示す文字あるいは フラグを導入する方法が一般的です． これから先の説明では，キーの終端を示す文字を終端文字， キーの終端を示すフラグを終端フラグと呼ぶことにします．

終端文字を導入する場合，文字列の末尾に終端文字をつけて登録するようにします． 例えば，終端文字を '#' で表すのであれば， "bird" の末尾に '#' をつけて，"bird#" にしてから登録するようにします． 終端文字があるおかげで，"bird#" は "birdie#" の前方部分でなくなり， "bird#" と対応する経路を辿ることで， 葉に到達することができるようになります． この方法の特徴は，登録されている文字列とトライの葉が一対一で対応することです． 四つの文字列 "bird", "birdie", "bison", "cat" を登録したトライに終端文字を導入すると，以下のようになります．

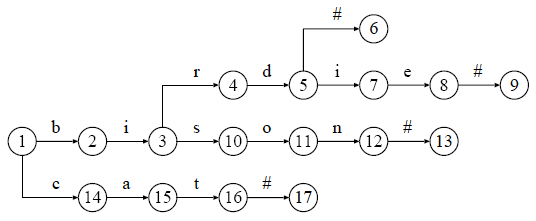
図 2 ： "bird", "birdie", "bison", "cat" を登録したトライに対する終端文字の導入例

終端フラグを導入する場合，すべての節に終端フラグを持たせます． そして，登録されている文字列を検索したとき，最終的に到達することになる 節の終端フラグだけを TRUE にします． なお，このような節のことを終端節と呼ぶことにします． 例えば，"bird" という文字列が登録されている場合， 'b', 'i', 'r', 'd' という順に対応する枝を辿ることで 到達する節の終端フラグを TRUE にします． トライが無駄な節の存在を許していない場合， すべての葉が終端節になります．

終端フラグを導入したトライでは，葉に到達するかどうかではなく， 探索終了時の節において，終端フラグが TRUE になっているかどうかを確認することで， 文字列が登録されているかどうかを確認します． そのため，登録されている他の文字列の前方部分になっているかどうかに関わらず， 同様の方法で登録されているかどうかを確認することができます． この方法の特徴は，登録されている文字列と終端節が一対一で対応することです． 四つの文字列 "bird", "birdie", "bison", "cat" を登録したトライに終端フラグを導入すると，以下のようになります．

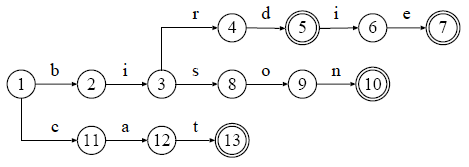
図 3 ： "bird", "birdie", "bison", "cat" を登録したトライに対する終端フラグの導入例

※ 終端フラグが TRUE の節は二重丸， FALSE の節は一重丸で表しています．

終端文字を導入した場合，キーの数だけ節が増加することになります． また，入力文字列の前方部分と一致するキーを得るためには， 節を移動するごとに，終端文字と対応する枝がないか確認する必要があります． しかし，すべての節を同様の構造で表現する場合， 葉において，枝を辿るための情報用に確保している領域を， レコード（ Record ）の格納などの 用途に流用することができます．

レコードというのは，キーに関連付けられた情報のことです． 単純なレコードの例としては，各キーに対する識別子 （ ID ）を挙げることができます． 他にも，索引語をキーとして，参照先の情報をレコードとするという用途や， 単語をキーとして，その単語の詳細情報をレコードとするという用途などがあります．

終端フラグを導入した場合，すべての節にフラグ用の領域が必要となりますが， 節の数は増加しません．結果として，終端文字を導入した場合よりも， 少ない領域でトライを実現することができます． また，探索時に到達した節の終端フラグを確認するだけで， 入力文字列の前方部分と一致するキーを得ることができます． しかし，レコードを必要とする場合，レコード用の領域を用意しなければなりません． そのため，単純なフィルタリングなどの用途において有効です．