Double-Array

ダブル配列（ Double-Array ）は， トライ（ Trie ）のデータ構造の一種であり， 小さい辞書で高速に検索できるという特長を持っています． 実際に，茶筌（ ChaSen ）や 和布蕪（ MeCab ）などの 形態素解析器で利用されているという実績があります．

ダブル配列では，配列を使ってトライを表現します． 配列の各要素が BASE, CHECK という二つの整数を持つので，頭文字をとって配列 BC と呼ぶことにします． 以降の説明では，配列 BC の要素 x の BASE, CHECK を それぞれ BC[x].BASE, BC[x].CHECK と記述します． 通常，BASE, CHECK は個別の配列として紹介されますが， 特に分割して考える必要がないので，このような説明にしました．

基本的に，配列 BC の各要素は トライの節と一対一で対応します． そのため，対応する要素と節に関しては， 要素番号と節番号が一致するものとして扱います． なお，配列 BC における要素番号が前提となり， トライにおける節番号が決定されます．

ダブル配列では，終端文字によりキーの終端を示すのが一般的です． 以下に，三つの文字列 "bird", "bison", "cat" を登録したトライとダブル配列の例を示します． 配列 CODE は，文字を整数に変換するための配列です． 例えば，文字 'c' は 4 に変換されます．

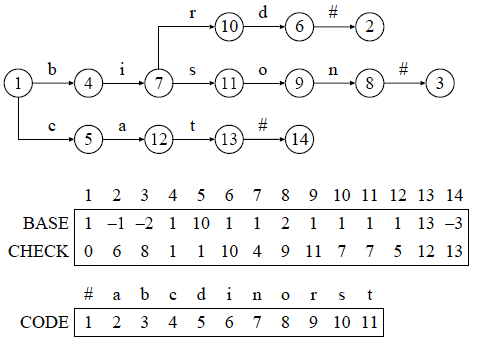
図 1 ： "bird", "bison", "cat" を登録したトライとダブル配列

節 x が葉である場合， BC[x].BASE はレコードを格納するために使用します． このとき，内部節と区別するため，マイナスの値を BC[x].BASE に格納するのが一般的です． 一方，節 x において， 文字 c と対応する枝が存在し， その枝を辿ることで節 y に到達する場合， BC[x].BASE + CODE[c] = y, BC[y].CHECK = x という関係が成立します． すなわち，文字に対応する整数と遷移元の BASE の和が遷移先の節番号と等しくなり，遷移先の CHECK が遷移元の節番号と等しくなります．

節 x において 文字 c と対応する枝を確認する場合， y = BC[x].BASE + CODE[c] により， 到達するはずの節 y を求めます． 次に，x と BC[y].CHECK が等しいかどうかを調べます． 枝が存在していれば等しくなり，枝が存在していなければ異なります．

検索の手順は，他のデータ構造を用いた場合と同様になります． 文字列が登録されているかどうかを確認する場合， その文字列を構成する文字と対応する枝を先頭から順に確認します． そして，葉に到達すれば文字列が登録されていることが分かり， 途中で枝の確認に失敗すれば文字列が登録されていないことが分かります． なお，節の移動時に終端文字と対応する枝を確認することによって． 入力文字列の前方部分と一致するキーを検出できます．

図 1 のダブル配列に 文字列 "bird" が登録されているかどうかを 確認する場合について説明します． 探索は，根である節 1 から始まります． 文字列 "bird" の一文字目である 文字 'b' と対応する枝があるかどうかを確認します． この例では，BC[1].BASE + CODE['b'] = 1 + 3 = 4 となるため，遷移先の候補は節 4 であることが分かります． さらに，BC[4].CHECK = 1 が成立することから， 節 4 への枝が確認できます． 同じように，BC[4].BASE + CODE['i'] = 1 + 6 = 7, BC[7].CHECK = 4 より，二文字目と対応する， 節 7 への枝が確認できます． 続けて節 10, 6, 2 と移動したところで， BC[2].BASE < 0 より， 葉に到達したことが分かります．

ダブル配列によるトライでは，枝の確認にかかる時間計算量が 係数の小さい O(1) になり， 各節（要素）が二つの整数のみによって構成されます． 結果として，配列構造と同じくらい高速で， リスト構造と同じくらいコンパクトになるとされています． 現在のところ，ダブル配列よりコンパクトに トライを実現できるデータ構造は複数ありますが， 検索速度においてダブル配列を超えるデータ構造は見当たりません．

ダブル配列の提案では，TAIL という配列を用いて 分岐をもたない節を除去する手法が述べられています． なお，この手法を適用したトライとダブル配列のことを， それぞれ Minimal Prefix （MP） トライや MP ダブル配列と呼んだり， （最小）接頭辞トライや（最小）接頭辞ダブル配列などと呼んだりします． 例として，図 1 のトライとダブル配列に対応する MP トライと MP ダブル配列を示します．

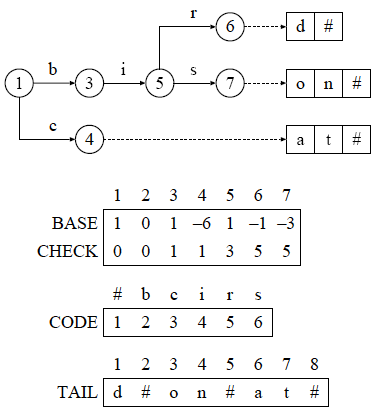
図 2 ： "bird", "bison", "cat" を登録した MP トライと MP ダブル配列

MP トライでは， 探索時にキーの候補を一つに絞り込む上で必要な節だけを残し， その他の節を文字として保存します． MP ダブル配列で 新たに使用する配列 TAIL は， この文字を格納するための配列です． 図 1 を例にすると， 節 2, 3, 6, 8, 9, 12, 13, 14 が除去対象となります． 図 2 では，除去対象の節への枝と対応する文字が， 配列 TAIL に格納されています． なお，キーの前方部分である文字列 "bir", "bis", "c" を接頭辞 （ Prefixes ）， キーの後方部分である文字列 "d#", "on#", "at#" を接尾辞（ Suffixes ）と呼ぶことがあります．

図 1, 2 を比較すると， 節の数が 14 から 6 に減っていることと，追加された配列 TAIL の要素数が 8 になっていることが分かります． また，除去した節を文字に置き換えるので， 節の数 14, 6 と TAIL の要素数 8 の間には， 14 - 6 = 8 という関係が成立しています．

この例では，節の減少や新たな配列の追加以外にも注目すべきことがあります． それは，図 2 の MP トライに 節 2 が存在しないことです． 配列 BC には要素 2 が存在しているので，対応する節を持たない要素があることになります． このような要素は，節として使用されないため， 未使用要素（ Empty Element ）と呼ばれます． また，実体が存在しない節 2 については， 幽霊節（ Ghost Node ）という呼び方があります．

図 2 の MP ダブル配列は， 図 1 のダブル配列と比べて， 配列 BC の要素数が 7 少なくなり，配列 TAIL の要素数が 8 多くなっています． 配列 BC の各要素は 二つの整数 BASE, CHECK により構成されるので， 整数を 4bytes， 文字を 1byte で表現する場合，差分は 7 × 8bytes − 8 × 1byte = 48bytes になります．